Drzewa ósemkowe

Jak już pisałem w moim pierwszym artykule na temat generatora świata który implementuję, jedną z możliwych struktur danych do przechowywania świata w pamięci komputera jest drzewo ósemkowe. Jako że użycie tej struktury pozwala zaoszczędzić dużo pamięci, w pierwszej kolejności zdecydowałem się na jej przetestowanie. W tym artykule chciałbym opisać mniej więcej moje próby oraz wyniki i wnioski związane z zastosowaniem tego rozwiązania.

Ponieważ wytłumaczyłem już jak działają i czym są drzewa ósemkowe (możesz o tym przeczytać w poprzednim artykule) tutaj zajmę się tylko moją implementacją i testami, które przeprowadziłem, czyli rzeczami bardziej związanymi z moim projektem niż samą teorią.

Pisząc moją implementację drzewa ósemkowego w znacznej mierze wzorowałem się na artykule Samuli Laine'a i Tero Karras'a z 2010 roku (dostępnym tutaj). Każda gałąź mojego drzewa zajmuje dokładnie 64 bity. W nich zapisane są informacje takie jak adres pierwszego z ośmiu dzieci danego węzła, maska mówiąca o tym ile istnieje dzieci danego węzła oraz dane z czego składa się opisywana przestrzeń. Poniższy obrazek prezentuje graficznie ułożenie danych wewnątrz gałęzi drzewa:

Adres pierwszego dziecka dla danego węzła nie jest zapisany w formie adresu bezwzględnego. Pierwsze 32 bity to przesunięcie względem początku bloku pamięci, a kolejne 8 bitów mówi o tym, który to blok. Dodatkowo, następne 8 bitów to maska bitowa, która informuje o tym, które dzieci węzła są aktualnie używane (w pozostałych miejscach mogą być nieokreślone dane). Dzięki temu można łatwo wyliczyć adres dowolnego dziecka danego węzła wzorem:

address = ptr + blockNr * BLOCK_SIZE + 8 * childNr;

Gdzie ptr to przesunięcie względne, blockNr to numer bloku w którym znajduje się pierwsze dziecko gałęzi, BLOCK_SIZE to rozmiar jednego bloku pamięci, a childNr to numer dziecka (odczytany z maski bitowej). Zapewnia to łatwy i szybki dostęp do dowolnego dziecka danego węzła.

Zaimplementowanie samego drzewa nie było większym problemem. Jednak bez możliwości wizualizacji tego drzewa trudno było stwierdzić czy wszystko działa prawidłowo i tak jak bym się tego spodziewał. Dlatego kolejnym krokiem było napisanie prostej wizualizacji. Okazało się, że i to zadanie nie było zbyt problematyczne, na wasze szczęście zresztą, bo dzięki temu teraz mogę pokazać kilka wizualizacji jakie udało mi się uzyskać, dla różnych przypadków testowych

Pierwszy przypadek jest bardzo prosty i ilustruje drzewo wypełnione w całości blokami z tego samego materiału. Nie jest to zbyt ciekawy przypadek (na pewno nie wizualnie), ale od czegoś musiałem zacząć, rozumiecie Co jest bardziej pocieszające, drzewo w tym przypadku sprawdza się o niebo lepiej niż tablica trójwymiarowa ponieważ wymaga utworzenia tylko jednej gałęzi i zajmuje jedynie 8 bajtów! (niestety to bardzo specyficzny przypadek)

Drugi przypadek przedstawia przestrzeń wypełnioną blokami jednego typu, z małą kostką w rogu która zbudowana jest z ośmiu kostek, z czego każda innego typu. Ten przypadek, choć nadal prosty, wygląda już nieco lepiej. Zaalokowane zostało łącznie 12 gałęzi co oznacza 96 bajtów zajętego miejsca, nadal niezły wynik

Kolejny przypadek testowy jest podobny do tego poprzedniego, z tym, że tutaj w całej przestrzeni znajdują się cztery małe kostki z innego materiału, każda w innym rogu. Zaalokowane zostało aż (albo tylko ) 25 węzłów, co oznacza zajętość pamięci na poziomie 200 bajtów. Bardzo daleko nam do nawet jednego kilobajta, a warto zwrócić uwagę, że tablica trójwymiarowa o rozmiarach 64x64x64 zajmowałaby ok. 0.5 MB w każdym z wymienionych przypadków.

Ostatni przypadek jaki chciałbym pokazać to przypadek w którym wygenerowana została powierzchnia w kształcie sinusoidy. Tym razem musiało powstać 3 439 węzłów. Wybaczcie moje lenistwo, ale nie będę nawet liczył ile to zajętych bajtów W każdym razie jest to ok. 0.08 MB, a to wciąż bardzo daleko od 0.5 MB jakie zajmuje pełna tablica.

To oczywiście nie wszystkie testy jakie przeprowadziłem. Nie mogło obyć się bez testu na pełne drzewo, gdzie każdy blok musi być opisany z osobna, bo nie jest możliwe połączenie żadnych ośmiu bloków. Nie chcę pokazywać jak wyglądało wtedy drzewo, bo i tak nic ciekawego nie byłoby widać (chyba, że interesuje was wielka zielona kostka złożona z gęstych linii). Mogę jednak powiedzieć, że pełne drzewo miało 168 521 węzłów i zajmowało ok. 2.29 MB, a to już bardzo zły wynik, bo ponad cztery razy gorszy niż pełna tablica! Oznacza to, że chociaż takie drzewo ma potencjał, to w najgorszym wypadku, okazuje się być o wiele gorsze niż tablica.

Po testach mojej nowo utworzonej struktury przyszła także pora na przetestowanie jej w akcji. Oznaczało to napisanie (albo przynajmniej próbę napisania) generatora, który wykorzystywałby drzewo ósemkowe, jako strukturę do przechowywania danych. Oczywiście udało mi się to zrobić, ale tutaj pojawił się pewien nieprzewidziany problem. O ile drzewo całkiem nieźle sprawdza się kiedy chodzi o oszczędność pamięci, niestety nieco gorzej jest z wydajnością jego działania... Po napisaniu prostego generatora i wizualizacji okazało się, że nawet generacja prostego, zupełnie płaskiego, świata stanowi problem. Wynikał on z szybkości generowania drzewa (a może bardziej "wolności"). Struktura ta niestety nie jest aż tak prosta jak zwykła tablica i wygenerowanie jej zajmuje trochę czasu. Byłoby to jeszcze akceptowalne, gdyby świat miał być zupełnie statyczny i nie można byłoby wprowadzać do niego żadnych zmian, ale nie jeśli świat w założeniu ma się dynamicznie zmieniać! Niestety dowolna zmiana wymagałaby utworzenia drzewa zupełnie od nowa, a patrząc na prędkość z jaką drzewo to się tworzyło, nie wpływałoby to najlepiej na grywalność (wygenerowanie nawet małej ilości płaskiego terenu zajmowało kilkanaście minut).

Pomimo tego, że drzewo nie sprawdziło się jako struktura do przechowywania świata w moim silniku (bo w końcu ten generator ma być częścią całego silnika) udało mi się dostać jako tako działającą aplikację. Niestety nie powalała szybkością, a kolejne kawałki świata wczytywały się zdecydowanie za wolno. Mogę jednak pokazać co udało mi się osiągnąć, kiedy już ostatecznie doczekałem się na wczytanie świata

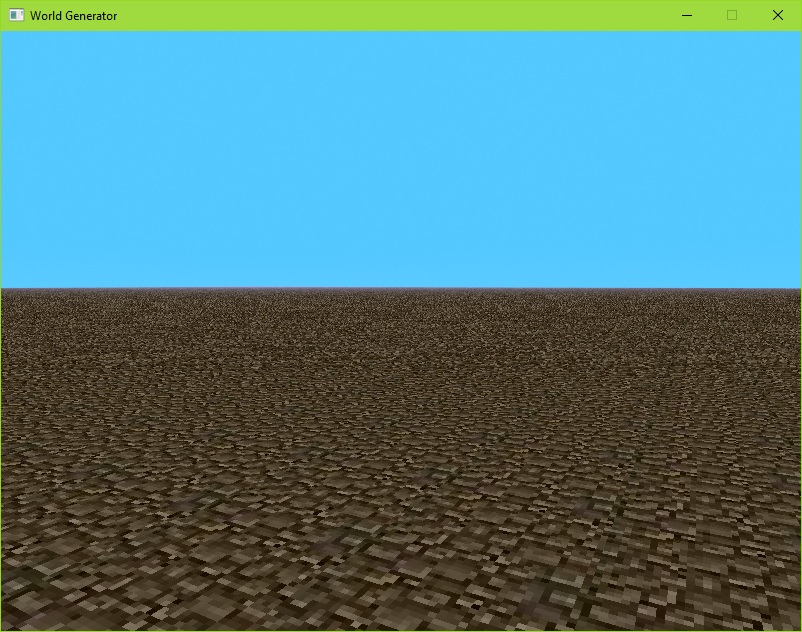
Nie jest to powalający widok. Myślę, że jest za pusto i za płasko tak jakby Raczej nikt nie chciałby mieszkać w takim miejscu, ale jak na jakieś pustkowie wygląda to nawet całkiem spoko

Tak więc podsumowując powyższe rozważania, testy i ogólnie wszystko co udało mi się dotychczas osiągnąć, można wyciągnąć wnioski. Drzewa ósemkowe, chociaż bardzo przydatne jako, że pozwalają oszczędzać znaczne ilości pamięci (w przeciętnych sytuacjach, w najgorszym wypadku są nawet dużo gorsze), a także umożliwiają łatwiejsze obliczenia np. przy rzutowaniu promieni, albo testowaniu kolizji, nie koniecznie sprawdzają się w świecie, który może być dynamicznie zmieniany. Tworzenie drzewa, jest dużo bardziej kosztowne, a dostęp do niego i przemieszczanie się po nim, także wnosi dodatkową złożoność.

Myślę, że jak na razie to koniec moich testów z tym typem struktury. Następną próbę podejmę jednak na zwykłych tablicach trójwymiarowych. W międzyczasie (podczas testów z drzewami, kiedy okazało się, że są zbyt wolne), szukałem w różnych źródłach, jak może działać taki silnik i w większości wypadków, komercyjne silniki opierają się jednak na tablicach. Wynika to z faktu, że tablice są o wiele szybsze a aktualnie pamięć RAM nie jest aż tak drogim zasobem i nawet zwykli użytkownicy mogą sobie pozwolić na duże jej ilości.

Jeśli jesteś zainteresowany jak dalej potoczy się los mojego projektu sprawdzaj regularnie blog na mojej stronie. W niedługim czasie postaram się zamieścić opis kolejnych postępów i moich prób, tym razem już ze zwykłymi tablicami